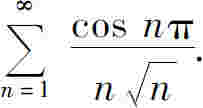上节介绍的收敛判别法仅适用于正项级数．本节讨论带负项的级数，其中简单而重要的一类是交错级数．
如果一个级数的各项是正负交错的，即形如
其中un＞0（n＝1，2，…），则称该级数为交错级数．
关于交错级数，有如下判别法：
则级数收敛，且其和s≤u1．
证 级数的前2n项部分和
级数的前2n＋1项部分和
s2n＋1＝s2n＋u2n＋1．
例1 讨论交错级数
的收敛性．
解 这里
由莱布尼茨判别法知级数收敛．
现在来讨论一般的级数
证 因为
解 因为
而级数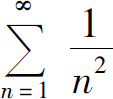
收敛，所以所给级数绝对收敛，因而收敛．
解
1．下列交错级数哪些收敛？哪些发散？
（3）
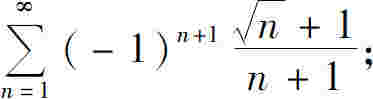
2．判定下列级数是否收敛？如果收敛，是绝对收敛还是条件收敛？
（6）
